在我开始学习计算机的时候有一种观点:数论是被看作有趣而无用的学问。 譬如说,概率论可以用来赌博,华罗庚的优选法可以用来蒸馒头,而数论在当时的认识中,只有类似数学体操的作用。后来随着计算机的发展,或者说自从有了互联网,眼界大开之后,惊奇的发现数论简直是现代计算机和互联网的基石,没有数论就没有办法发展出来压缩算法,同样也没有办法发展出各种加密方法。
OpenSSL 库中提供的大数运算功能,这次我们就使用 CryptoPkg进行实验。
本文调用的 OpenSSL 函数可以在 【参考1】和【参考2】中看到,非常感谢作者用通俗的语言展示了他们的使用方法。
本次的代码需要放置在CryptoPkg中进行编译,编译后的 Application可以直接在 Nt32环境下运行。
代码如下:
#include <Uefi.h>
#include <Library/UefiLib.h>
#include <Library/MemoryAllocationLib.h>
#include <Library/BaseMemoryLib.h>
#include <stdlib.h>
#include <Library/BaseLib.h>
#include <Library/BaseCryptLib.h>
#include <Library/OpensslLib/openssl/crypto/bn/bn_lcl.h>
#include <Library/OpensslLib/openssl/include/openssl/err.h>
#include <Library/OpensslLib/openssl/include/openssl/rand.h>
extern EFI_BOOT_SERVICES *gBS;
CONST CHAR8 str[]="0x1234567890ABCDEF1234567890ABCDEF";
CHAR16 strCH16[]=L"0x1234567890ABCDEF1234567890ABCDEF1234567890ABCDEF1234567890ABCDEF";
CONST CHAR8 aStr[]="193707721";
CONST CHAR8 bStr[]="761838257287";
EFI_STATUS
EFIAPI
main (
IN EFI_HANDLE ImageHandle,
IN EFI_SYSTEM_TABLE *SystemTable
)
{
BIGNUM *a,*b;
CHAR8 *show;
BN_CTX *ctx;
// New a big munber
a=BN_new();
// Set a as 1
BN_one(a);
// Show a as DEC
show = BN_bn2dec(a);
AsciiStrToUnicodeStr(show,strCH16);
Print(L"BN_bn2dec %s\n",strCH16);
OPENSSL_free(show);
// Show a as HEX
show = BN_bn2hex(a);
AsciiStrToUnicodeStr(show,strCH16);
Print(L"BN_bn2hex %s \n",strCH16);
OPENSSL_free(show);
b=BN_new();
// Assign aStr to a
BN_dec2bn(&a,aStr);
// Assign aStr to b
BN_dec2bn(&b,bStr);
ctx=BN_CTX_new();
// Mul a with b, result in a
BN_mul(a,a,b,ctx);
// add a with 1
BN_add_word(a,1);
BN_CTX_free(ctx);
// Show a in Hex
show = BN_bn2hex(a);
AsciiStrToUnicodeStr(show,strCH16);
Print(L"BN_bn2hex %s \n",strCH16);
OPENSSL_free(show);
return EFI_SUCCESS;
}
INF 文件
## @file # A simple, basic, application showing how the Hello application could be # built using the "Standard C Libraries" from StdLib. # # Copyright (c) 2010 - 2011, Intel Corporation. All rights reserved.<BR> # This program and the accompanying materials # are licensed and made available under the terms and conditions of the BSD License # which accompanies this distribution. The full text of the license may be found at # http://opensource.org/licenses/bsd-license. # # THE PROGRAM IS DISTRIBUTED UNDER THE BSD LICENSE ON AN "AS IS" BASIS, # WITHOUT WARRANTIES OR REPRESENTATIONS OF ANY KIND, EITHER EXPRESS OR IMPLIED. ## [Defines] INF_VERSION = 0x00010006 BASE_NAME = bignumtest FILE_GUID = 4ea97c46-7491-4dfd-0082-747010f3ce5f MODULE_TYPE = UEFI_APPLICATION VERSION_STRING = 0.1 ENTRY_POINT = main # # VALID_ARCHITECTURES = IA32 X64 IPF # [Sources] BigNumTest.c [Packages] MdePkg/MdePkg.dec CryptoPkg/CryptoPkg.dec [LibraryClasses] UefiApplicationEntryPoint UefiLib BaseCryptLib
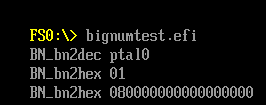
运行结果:
结果的第一行,展示的是 BN_bn2dec 函数将 a (值为1)转化为 string 显示的结果。非常遗憾,这个结果明显不正确。我尝试使用最新的 OpenSSL Source ,仍然是这样的结果,不知道是什么地方出现的问题。
结果的第二行,显示的是使用 BN_bn2hex函数显示a的十六进制结果,是正确的。
接下来代码使用 BN_dec2bn 函数将自定义的十进制字符串转换为一个大数,经过计算最终显示193707721*761838257287 + 1 的十六进制结果,是 0x8 0000 0000 0000 0000,也就是 2^67。关于这个数字,有下面的典故:
17世纪有位法国数学家叫梅森(Marin Mersenne,1588–1648),他曾经做过一个猜想:2^p-1 ,当p是质数时,2^p-1是质数。他验算出了:当p=2、3、5、7、17、19时,所得代数式的值都是质数,后来,欧拉证明p=31时,2^p-1是质数。 p=2,3,5,7时,2^p-1都是素数,但p=11时,所得2047=23×89却不是素数。还剩下p=67、127、257三个梅森数,由于太大,长期没有人去验证。
1903年10月,在美国纽约举行的世界数学年会上,一个叫科尔的数学家(Frank Nelson Cole),面对满场等待他学术报告的听众,一言不发,径直走向黑板,写下了一个等式:
2^67 – 1 = 193707721×767838257287 = 147,573,952,589,676,412,927
在一阵寂静之后,台下突然爆发出热烈的掌声。更令人惊奇的是,科尔并不是专门研究数论的数学家,这只是他的业余爱好。
后来有人问他:“您论证这道题目花了多长时间?”
他回答说:“3年来的全部星期天。”
和很多哲理小故事一样,上面的写的如同段子一样。不过也许 WIKI 上面的一句话可以作为上面小故事结尾的佐证吧:“Cole died alone in New York City, aged 64.”【参考3】
参考:
1. http://www.qmailer.net/archives/216.html
2. https://blog.csdn.net/qq_30866297/article/details/51470991
3. https://en.wikipedia.org/wiki/Frank_Nelson_Cole
4. https://www.mobilefish.com/services/big_number_equation/big_number_equation.php#equation_output 一个在线进行大数运算的网页,可以用来验证结果是否正确