本文会介绍关于 RSA 算法的基础知识和一些简单的实验。行文力求通俗易懂,期望没有 UEFI 相关知识的朋友也能够读懂。文章涉及到一些密码方面的内容,是根据自己的理解进行描述,因此会存在不准确的情况,请读者在阅读过程中注意批判。
最容易的理解的密码是对称式的密码,加密解密是同样的密码。但在实际使用上,加密方如何将密码传递给解密方是一个严重的问题。比如,我设置了一个密码,然后告诉对方这是《和张仆射塞下曲》的前两句的拼音首字母“月黑雁飞高,单于夜遁逃”。对方尝试了很久都没有效果,我只能告诉他是“yhyfgdyydt”【参考1】…….当然相比对方理解出现问题,更容易出现问题的环节是密码在传递过程中被第三方截获。因此,我们在诸多谍战片中常常看到双方为了争夺密码本展开殊死搏斗。
为了克服对称式密码的缺陷,RSA横空出世。“RSA公钥加密算法是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。1987年7月首次在美国公布,当时他们三人都在麻省理工学院工作实习。RSA就是他们三人姓氏开头字母拼在一起组成的。”【参考2】
简单的说RSA 的原理就是“对两个质数相乘容易,而将其合数分解很难的这个特点进行的加密算法”【参考3】。
在使用上,RSA算法将密码分成2部分,公钥和私钥。一个典型的应用场景是:我想接受别人发给我的秘密消息,那么我可以生成一套公钥和私钥。私钥留在自己手上,公钥放在我的网站上。任何人想给我发送秘密的内容,可以先到网站获取公钥,然后用公钥加密消息,再通过 eMail之类的发送密文给我,收到消息之后,我用私钥解密然后就获得了消息明文。在这个过程中,如果有人截获了加密后的密文,在有公钥和密文的情况下仍然无法得到原文。通过这样的方式达到保密通讯的目的。
上面是对于这个算法的简单介绍,下面通过一系列实验来展示这个算法的使用。
通过在线的RSA生成工具进行实验. 在http://web.chacuo.net/netrsakeypair 生成一对公钥和私钥(这是随机生成的)
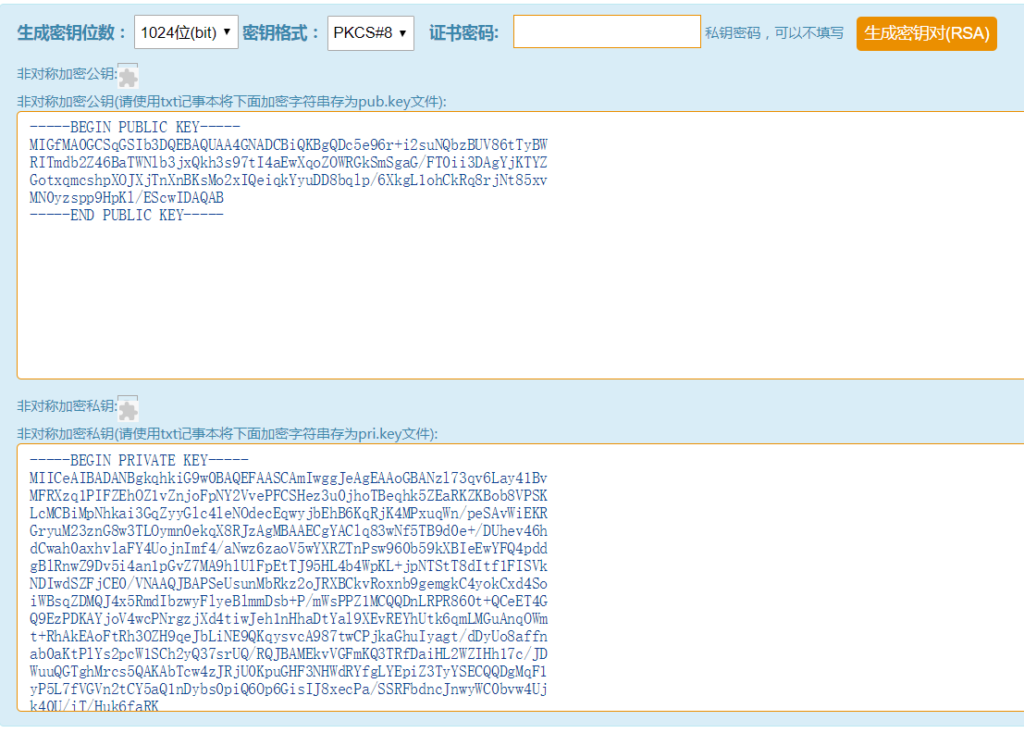
上面生成的公钥和私钥:
公钥如下
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDc5e96r+i2suNQbzBUV86tTyBW
RITmdb2Z46BaTWNlb3jxQkh3s97tI4aEwXqoZOWRGkSmSgaG/FT0ii3DAgYjKTYZ
GotxqmcshpXOJXjTnXnBKsMo2xIQeiqkYyuDD8bqlp/6XkgL1ohCkRq8rjNt85xv
MN0yzspp9HpKl/EScwIDAQAB
-----END PUBLIC KEY-----
私钥如下:
-----BEGIN PRIVATE KEY-----
MIICeAIBADANBgkqhkiG9w0BAQEFAASCAmIwggJeAgEAAoGBANzl73qv6Lay41Bv
MFRXzq1PIFZEhOZ1vZnjoFpNY2VvePFCSHez3u0jhoTBeqhk5ZEaRKZKBob8VPSK
LcMCBiMpNhkai3GqZyyGlc4leNOdecEqwyjbEhB6KqRjK4MPxuqWn/peSAvWiEKR
GryuM23znG8w3TLOymn0ekqX8RJzAgMBAAECgYAClq83wNf5TB9d0e+/DUhev46h
dCwah0axhvlaFY4UojnImf4/aNwz6zaoV5wYXRZTnPsw960b59kXBIeEwYFQ4pdd
gBlRnwZ9Dv5i4an1pGvZ7MA9hlUlFpEtTJ95HL4b4WpKL+jpNTStT8dItf1FISVk
NDIwdSZFjCE0/VNAAQJBAPSeUsunMbRkz2oJRXBCkvRoxnb9gemgkC4yokCxd4So
iWBsqZDMQJ4x5RmdIbzwyFlyeBlmmDsb+P/mWsPPZ1MCQQDnLRPR860t+QCeET4G
Q9EzPDKAYjoV4wcPNrgzjXd4tiwJeh1nHhaDtYal9XEvREYhUtk6qmLMGuAnqOWm
t+RhAkEAoFtRh3OZH9qeJbLiNE9QKqysvcA987twCPjkaGhuIyagt/dDyUo8affn
ab0aKtPlYs2pcW1SCh2yQ37srUQ/RQJBAMEkvVGFmKQ3TRfDaiHL2WZIHh17c/JD
WuuQGTghMrcs5QAKAbTcw4zJRjU0KpuGHF3NHWdRYfgLYEpiZ3TyYSECQQDgMqF1
yP5L7fVGVn2tCY5aQ1nDybs0piQ6Op6GisIJ8xecPa/SSRFbdncJnwyWC0bvw4Uj
k40U/iT/Huk6faRK
-----END PRIVATE KEY-----
接下来, 去http://tool.chacuo.net/cryptrsapubkey 使用上面的公钥对 “www.lab-z.com” 这段字符串进行加密(需要把上面生成的公钥拷贝粘贴到公钥框中,然后点击RSA公钥加密):
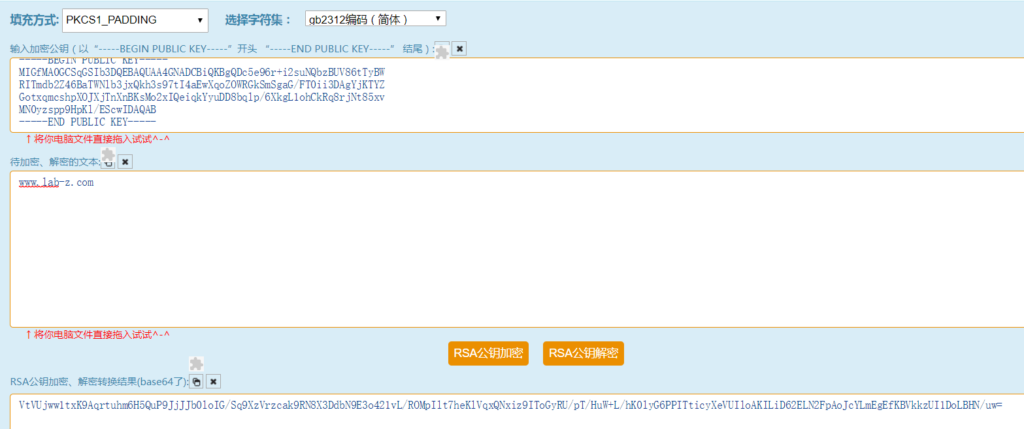
得到密文如下:
“VtVUjww1txK9Aqrtuhm6H5QuP9JjJJb0loIG/Sq9XzVrzcak9RN8X3DdbN9E3o421vL/ROMpIlt7heKlVqxQNxiz9IToGyRU/pT/HuW+L/hK0lyG6PPITticyXeVUIloAKILiD62ELN2FpAoJcYLmEgEfKBVkkzUI1DoLBHN/uw=”
再接下来, 实验用私钥对上面的密文进行解密。到http://tool.chacuo.net/cryptrsaprikey 页面, 将最开始生成的私钥粘贴到里面, 然后粘贴上面的密文. 最后点击RSA私钥解密即可得到原文。
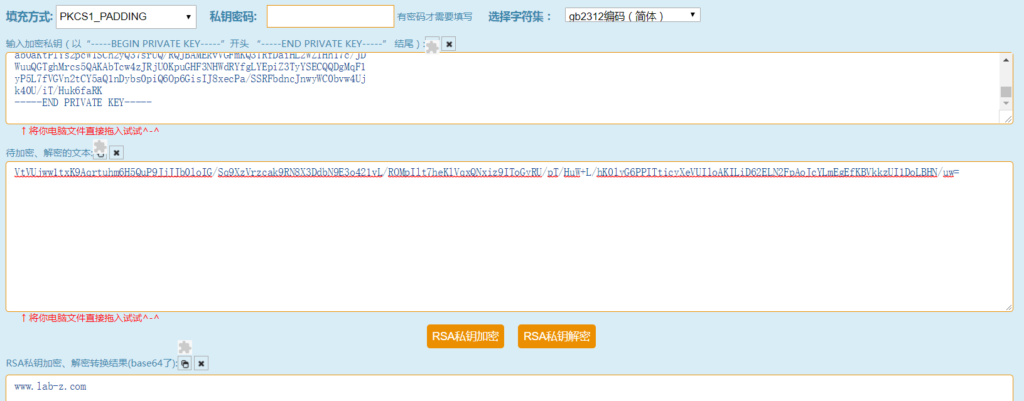
上面是一个完整的RSA加密解密的例子。在 RSA 中,还可以使用私钥来进行加密,加密之后的密文可以使用公钥来进行解密。因此,RSA 还可以用来进行身份验证。例如:我可以用私钥来加密一段信息,然后将密文发布在网站上。用户用公钥可以对密文进行解密。如果能够解密,就可以证明这段话确实是私钥拥有者发出来的。也正是如此,所以对于大多数自称“中本聪”而又无法用私钥来证明自己身份的人(无需Show出完整的私钥,只要公布一段私钥签名后的密文足矣),观众完全可以一笑了之。
目前业界通用的做法是使用 OpenSSL 来生成密钥对以及加密解密。OpenSSL中RSA私钥文件生成命令为:
openssl genrsa -out private_rsa.pem 1024
生成RSA公钥命令为:
openssl rsa -in private_rsa.pem -pubout -out public_rsa.pem
在openssl中执行以下命令,将BASE64编码的文件装换成二进制编码:
openssl base64 -d -in private_rsa.pem -out private.pem
也可以直接使用OpenSSL命令以明文形式输出密钥的各个参数值,例如:
openssl rsa -in private_rsa.pem -text -out private.txt
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDc5e96r+i2suNQbzBUV86tTyBW
RITmdb2Z46BaTWNlb3jxQkh3s97tI4aEwXqoZOWRGkSmSgaG/FT0ii3DAgYjKTYZ
GotxqmcshpXOJXjTnXnBKsMo2xIQeiqkYyuDD8bqlp/6XkgL1ohCkRq8rjNt85xv
MN0yzspp9HpKl/EScwIDAQAB
-----END PUBLIC KEY-----
-----BEGIN PRIVATE KEY-----
MIICeAIBADANBgkqhkiG9w0BAQEFAASCAmIwggJeAgEAAoGBANzl73qv6Lay41Bv
MFRXzq1PIFZEhOZ1vZnjoFpNY2VvePFCSHez3u0jhoTBeqhk5ZEaRKZKBob8VPSK
LcMCBiMpNhkai3GqZyyGlc4leNOdecEqwyjbEhB6KqRjK4MPxuqWn/peSAvWiEKR
GryuM23znG8w3TLOymn0ekqX8RJzAgMBAAECgYAClq83wNf5TB9d0e+/DUhev46h
dCwah0axhvlaFY4UojnImf4/aNwz6zaoV5wYXRZTnPsw960b59kXBIeEwYFQ4pdd
gBlRnwZ9Dv5i4an1pGvZ7MA9hlUlFpEtTJ95HL4b4WpKL+jpNTStT8dItf1FISVk
NDIwdSZFjCE0/VNAAQJBAPSeUsunMbRkz2oJRXBCkvRoxnb9gemgkC4yokCxd4So
iWBsqZDMQJ4x5RmdIbzwyFlyeBlmmDsb+P/mWsPPZ1MCQQDnLRPR860t+QCeET4G
Q9EzPDKAYjoV4wcPNrgzjXd4tiwJeh1nHhaDtYal9XEvREYhUtk6qmLMGuAnqOWm
t+RhAkEAoFtRh3OZH9qeJbLiNE9QKqysvcA987twCPjkaGhuIyagt/dDyUo8affn
ab0aKtPlYs2pcW1SCh2yQ37srUQ/RQJBAMEkvVGFmKQ3TRfDaiHL2WZIHh17c/JD
WuuQGTghMrcs5QAKAbTcw4zJRjU0KpuGHF3NHWdRYfgLYEpiZ3TyYSECQQDgMqF1
yP5L7fVGVn2tCY5aQ1nDybs0piQ6Op6GisIJ8xecPa/SSRFbdncJnwyWC0bvw4Uj
k40U/iT/Huk6faRK
-----END PRIVATE KEY-----
公钥
公钥指数及模数信息:
key长度: 1024
模数: DCE5EF7AAFE8B6B2E3506F305457CEAD4F20564484E675BD99E3A05A4D63656F78F1424877B3DEED238684C17AA864E5911A44A64A0686FC54F48A2DC30206232936191A8B71AA672C8695CE2578D39D79C12AC328DB12107A2AA4632B830FC6EA969FFA5E480BD68842911ABCAE336DF39C6F30DD32CECA69F47A4A97F11273
指数: 65537 (0x10001)
有兴趣的朋友可以在 http://www.lab-z.com/openssl-for-windows/ 找到一个 Windows 版本的 Open(当然这样的操作很不安全,最好是自己下载源代码进行编译。信息安全技术和传统文化一样,总是能找到“喷点”,譬如,高考语文是大众唯一能够热烈讨论的科目。春晚上的春联一定会被人找到不合时宜之处。)
RSA 算法的缺陷主要是加密速度很慢(RSA的速度是对应同样安全级别的对称密码算法的1/1000左右【参考1】)。因此,通常是和对称加密算法结合起来使用。比如:使用 RSA 算法传递一个足够长的密码,然后用DES 之类的使用这个密码进行加密和解密。
有一段时间,出于军事原因,加密算法属于美国政府的出口管制项目,但是随着英特网的蓬勃发展,加密技术变得无处不在,很多之前的机密算法也逐渐变得公开。有兴趣的朋友可以在【参考4】读到关于这方面的历史。
另外,还有一个很有趣的事情。RSA 算法本身足够安全,但是 RSA 密码对的生成未必是安全的。“援引路透社报道根据斯诺登泄漏的文件称受国家标准委员会NIST批准,美国美国安全局(NSA)和加密公司RSA达成了价值超过$1000万的协议,要求在移动终端中广泛使用的加密技术中放置后门,能够让NSA通过随机数生成算法Bsafe的后门程序轻易破解各种加密数据。对此RSA否认了相关的内容,声 称自己的加密算法只使用了国家认证的协议。而NSA则拒绝发表评论。
RSA Security是由RSA算法的发明者Ron Rivest, Adi Shamir和Len Adleman在1982年创立,随后在2006年以21亿美元的价格被EMC公司收购。其中该算法最为有名的一个缺陷就是DUAL_EC_DRBG,密码学家早在几年前就发现了这个问题。这个加密算法可以看作是随机数生成器,但是有些数字是固定的,密码学家能够将其作为万能钥匙通过一些内置的算法进行破解。
我们知道RSA算法本身没什么问题,因为只要你的密钥是真正随机产生的,猜对这个密钥就如同大海捞针一般难,现有计算机肯定无法在密码更换周期内攻破你的加密档案。但是,如果这个随机算法是假的呢?如果它仅仅是在一个很小的集合中产生的密钥呢?你的加密档案瞬间就被查看了,这就是NSA干的事情。”【参考5】
下次,我会介绍如何在 UEFI Shell 中实现一个简单的 RSA 加密和解密。
参考:
- “月黑雁飞高,单于夜遁逃” 其中的“单于”发音是Chán yú;我以为念成“dàn yú”,所以对方无法解密。
- https://baike.baidu.com/item/RSA 算法
- https://www.zhihu.com/question/25038691?sort=created RSA 算法的加密原理是什么?
- https://en.wikipedia.org/wiki/Export_of_cryptography_from_the_United_States
- https://www.williamlong.info/archives/3699.html路透社称NSA向RSA加密算法中放置后门